久しぶりにこちらのブログに。何ヶ月ぶりだろ、、4ヶ月ぶりか。
奥村先生のサイトに分割表の検定方法を比較しているページがありました。
Fisherの正確検定かカイ2乗検定か
フィッシャーの正確検定か? ピアソンのカイ二乗か?
巷の解説では、「フィッシャーの正確検定はパターンの数え上げに基づいているから正確だ。使用できる場合はいつでも使用すべき。」のような文言も見られますが、上のページを見れば正しくないと分かります!
上のページでは、総度数だけ固定される場合と周辺度数が完全に固定される場合を、それぞれunconditional/conditionalとして検討しています。
分割表の生成ルールは、どんな現象からどんな実験計画でデータをとったかによって変わります。
- 度数が非固定の場合
- 総度数が固定の場合
- 各行の度数が固定の場合
- 各行・各列の度数が固定の場合
この4つについてシミュレーションを追試してみます。ソースの全体は記事の最後にあります。
度数が非固定の場合
総度数含め度数が一切固定されない。
| 列1 | 列2 | ||
|---|---|---|---|
| 行1 | ○ | ○ | 行1合計 |
| 行2 | ○ | ○ | 行2合計 |
| 列1合計 | 列2合計 | 全合計 |
一定時間内の観測データなどがあたりそうです。実験のたびに標本サイズnが揺らぐのが特徴です。
セルの度数は独立なポアソン分布×4に従うと考えます。セルごとに平均(期待度数)のパラメータがあります。
| |
|
| |
|
パラメータ間に制約は設けないので、自由度は4。
総度数が固定の場合
全セルの度数の合計が決まっている。
| 列1 | 列2 | ||
|---|---|---|---|
| 行1 | ○ | ○ | 行1合計 |
| 行2 | ○ | ○ | 行2合計 |
| 列1合計 | 列2合計 | 全合計 |
決められた数の観測を行ったり、被験者数が事前に決まっているときはこれです。
セルの度数は多項分布に従うと考えます。セルごとに確率パラメータがあって、n回試行した結果の分布です。
| |
|
| |
|
(ただし、 )
パラメータは見た目4つでも、3つ決まれば残り1つは自動的に決まり、自由度は3。
行と列の独立条件
総度数が固定の場合の独立モデルは、多項分布の確率パラメータのオッズ比が1になるように制限します。
セルの確率が行と列の確率の積の形に表せるということです。
この制約で自由に動かせるパラメータが減って、自由度は2。
各行の度数が固定の場合
各行にあるセルの度数の合計が決まっている。
| 列1 | 列2 | ||
|---|---|---|---|
| 行1 | ○ | ○ | 行1合計 |
| 行2 | ○ | ○ | 行2合計 |
| 列1合計 | 列2合計 | 全合計 |
新薬の臨床試験で、新薬を投与するグループと従来薬を投与するグループの人数が決まっているときとか……。
列を「改善なし/あり」とすると、各列の度数は固定されないと考えられます。
セルの度数は行ごとに二項分布に従うとし、確率パラメータは同じとは限らない設定です。
- 1行目
| |
|
- 2行目
| |
|
パラメータはと
の2つ。パラメータ間の制約はないので、自由度は2。
行と列の独立条件
列の確率がどちらの行でも同じなら独立といえます。
つまり、1行目と2行目の二項分布の確率パラメータが等しいのが条件です。
この制約で自由に動かせるパラメータが減って、自由度は1。
各行・各列の度数が固定の場合
周辺度数(各行の度数、各列の度数、総度数)が完全に決まっている。
| 列1 | 列2 | ||
|---|---|---|---|
| 行1 | ○ | ○ | 行1合計 |
| 行2 | ○ | ○ | 行2合計 |
| 列1合計 | 列2合計 | 全合計 |
奥村先生のページでconditionalと呼ばれているモデルです。
セルの度数は左上のセルが超幾何分布に従って、残りのセルは自動的に決まります。
推定が必要なパラメータはなく、自由度は0……と思いきや、黒木玄先生のツイートによると1ですか。。うむむ。
#数楽 #統計 #JuliaLang
— 黒木玄 Gen Kuroki (@genkuroki) 2017年9月20日
サンプルを生成する確率分布の4×Poisson分布、多項分布、2×二項分布、超幾何分布ではそれぞれ乱数の自由度が4,3,2,1です。Fisherの正確検定で正確に計算される確率は超幾何分布の場合の確率で、他の場合はもちろん正確ではないです。
ここから、シミュレーション開始です!
ピアソンのカイ二乗検定(補正なし)
まず一番ポピュラーなピアソンのカイ二乗。
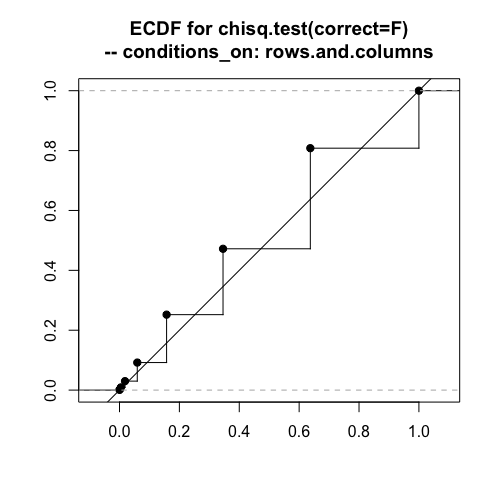
独立条件(下表の期待度数)で分割表を生成して、p値の一様性を評価します。点が斜め45度の線上に並ぶのが理想的な検定です。
| 45 | 15 |
| 30 | 10 |
# 1000回繰り返す trials = 1000 pearson_p_values = numeric(trials) for (i in 1:trials) { data = matrix(rtable_2x2(45,15,30,10,conditions_on="total"), ncol=2,byrow=T) pearson_p_values[i] = chisq.test(data,correct=F)$p.value } plot(ecdf(pearson_p_values),asp=1,xlab="", ylab="", xlim=c(0,1),ylim=c(0,1),verticals=TRUE, main="ECDF for chisq.test(correct=F)\n-- conditions_on: total") abline(0,1)
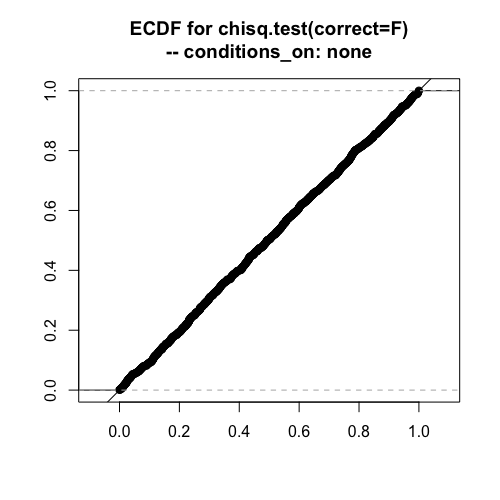
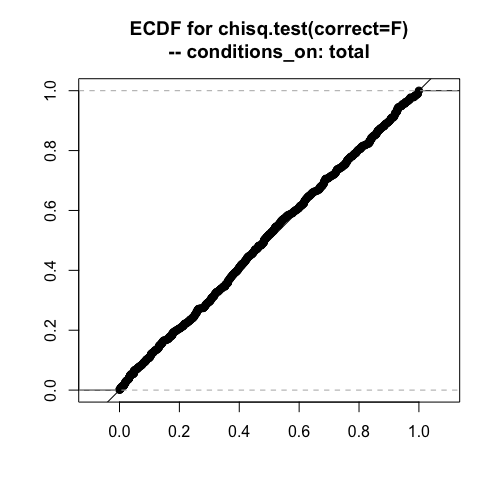
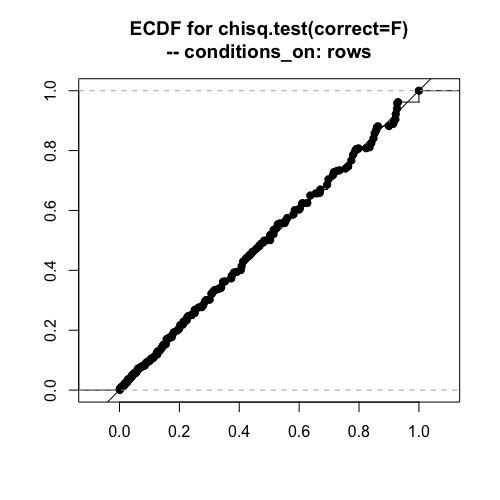
度数が揺らぐ場合や、各行の度数が固定される場合でも、ピアソンのカイ二乗は問題なく使用できそうです。
周辺度数が完全に固定される場合だけ、上にずれています。棄却域を設定する0の近くで傾きが大きくなっていて危険率が上がっています。
イェーツの連続性補正あり
# 1000回繰り返す trials = 1000 yates_p_values = numeric(trials) for (i in 1:trials) { data = matrix(rtable_2x2(45,15,30,10,conditions_on="total"), ncol=2,byrow=T) yates_p_values[i] = chisq.test(data,correct=T)$p.value } plot(ecdf(yates_p_values),asp=1,xlab="", ylab="", xlim=c(0,1),ylim=c(0,1),verticals=TRUE, main="ECDF for chisq.test(correct=T)\n-- conditions_on: total") abline(0,1)


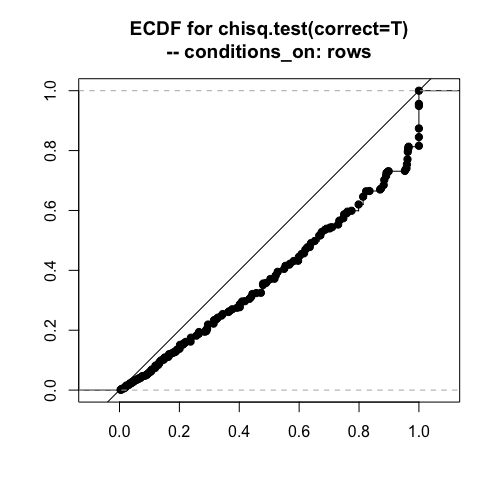

周辺度数が完全に固定される場合に線上に並んでいます。それ以外では、下にずれているので保守的(鈍感)に。
「連続性補正(correction for continuity)」の呼び方は歴史的な誤解かもしれません。むしろ小標本の方が、ずれがひどい。。
フィッシャーの正確検定
# 1000回繰り返す trials = 1000 fisher_p_values = numeric(trials) for (i in 1:trials) { data = matrix(rtable_2x2(45,15,30,10,conditions_on="total"), ncol=2,byrow=T) fisher_p_values[i] = fisher.test(data)$p.value } plot(ecdf(fisher_p_values),asp=1,xlab="", ylab="", xlim=c(0,1),ylim=c(0,1),verticals=TRUE, main="ECDF for fisher.test()\n-- conditions_on: total") abline(0,1)
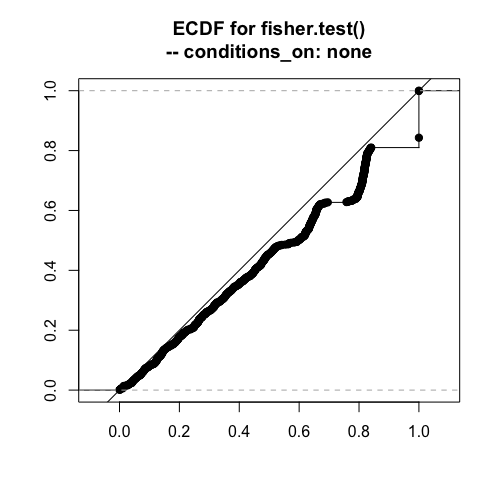
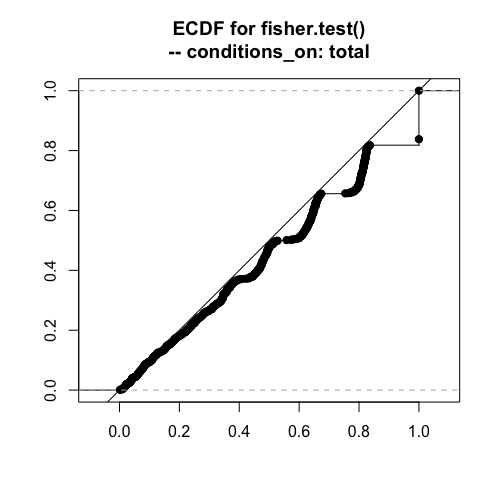
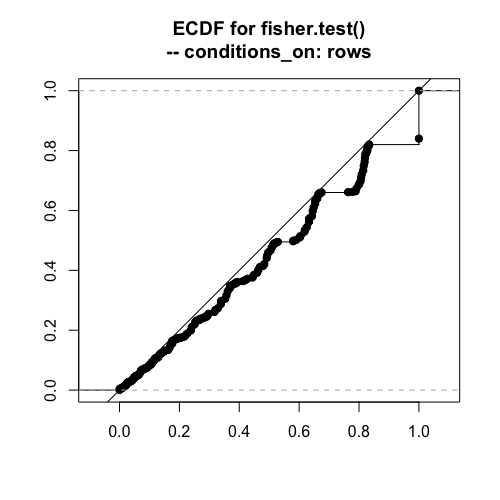
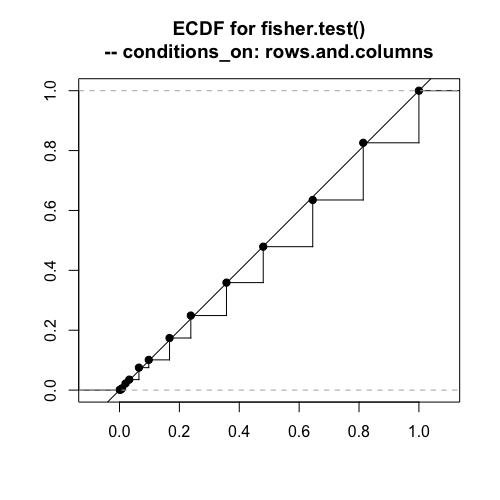
傾向はイェーツのカイ二乗と同じ感じです。この検定が正確なのは、周辺度数が完全に固定される場合ですね。この場合は、近似が入らないフィッシャーの方法が最適と考えられます。
奥村先生のページに「(Fisherの方法を)近似するものとして連続性の補正をしたカイ2乗検定があります。」と書かれていました。
G検定
対数線形モデルの尤度比検定だから、glm関数でいけそう……?(マニュアルにあたらないと、、)
ソース
最後に、2×2分割表を生成するRのソースです。
# 2×2分割表 # 各セルの期待度数:a, b, c, d # 度数の固定:conditions_on # ="none" 度数を固定しない # ="total" 総度数を固定(初期値) # ="rows" 各行の度数を固定(総度数も固定) # ="columns" 各列の度数を固定(総度数も固定) # ="rows.and.columns" 各行・各列の度数を固定(総度数も固定) rtable_2x2 = function(a, b, c, d, conditions_on = "total") { if (min(a, b, c, d) < 0) { # 期待度数は非負でないとだめ print("Illegal argument!") return() } switch(conditions_on, "none" = return(rtable_2x2_n(a, b, c, d)), "total" = return(rtable_2x2_t(a, b, c, d)), "rows" = return(rtable_2x2_r(a, b, c, d)), "columns" = return(rtable_2x2_c(a, b, c, d)), "rows.and.columns" = return(rtable_2x2_rc(a, b, c, d)), { # その他の値はエラー print("Illegal argument!") return() } ) } rtable_2x2_n = function(a, b, c, d) { # 乱数(ポアソン×4) counts = integer(4) counts[1] = rpois(1, lambda = a) counts[2] = rpois(1, lambda = b) counts[3] = rpois(1, lambda = c) counts[4] = rpois(1, lambda = d) return(counts) } rtable_2x2_t = function(a, b, c, d) { n = a + b + c + d # 総度数 # 乱数(多項) counts = rmultinom(1, size = n, prob = c(a, b, c, d) / n) return(counts) } rtable_2x2_r = function(a, b, c, d) { r1 = a + b # 1行目の度数 r2 = c + d # 2行目の度数 # 乱数(二項×2) counts = integer(4) counts[1] = rbinom(1, size = r1, prob = a / r1) counts[2] = as.integer(r1 - counts[1]) counts[3] = rbinom(1, size = r2, prob = c / r2) counts[4] = as.integer(r2 - counts[3]) return(counts) } rtable_2x2_c = function(a, b, c, d) { c1 = a + c # 1列目の度数 c2 = b + d # 2列目の度数 # 乱数(二項×2) counts = integer(4) counts[1] = rbinom(1, size = c1, prob = a / c1) counts[2] = rbinom(1, size = c2, prob = b / c2) counts[3] = as.integer(c1 - counts[1]) counts[4] = as.integer(c2 - counts[2]) return(counts) } rtable_2x2_rc = function(a, b, c, d) { r1 = a + b # 1行目の度数 r2 = c + d # 2行目の度数 c1 = a + c # 1列目の度数 # 乱数(超幾何) counts = integer(4) counts[1] = rhyper(1, m = r1, n = r2, k = c1) counts[2] = as.integer(r1 - counts[1]) counts[3] = as.integer(c1 - counts[1]) counts[4] = as.integer(r2 - counts[3]) return(counts) }
# 1000回繰り返す trials = 1000 pearson_p_values = numeric(trials) yates_p_values = numeric(trials) fisher_p_values = numeric(trials) for (i in 1:trials) { data = matrix(rtable_2x2(45,15,30,10,conditions_on="total"), ncol=2,byrow=T) pearson_p_values[i] = chisq.test(data,correct=F)$p.value yates_p_values[i] = chisq.test(data,correct=T)$p.value fisher_p_values[i] = fisher.test(data)$p.value }